Matthew Bennett

I am a data scientist working on time series forecasting (using R and Python 3) at the London Ambulance Service NHS Trust. I earned my PhD in cognitive neuroscience at the University of Glasgow working with fmri data and neural networks. I favour linux machines, and working in the terminal with Vim as my editor of choice.
View the Project on GitHub Dr-Matthew-Bennett/Matt-A-Bennett.github.io
Full Code
Below is all the code that we have written to date.
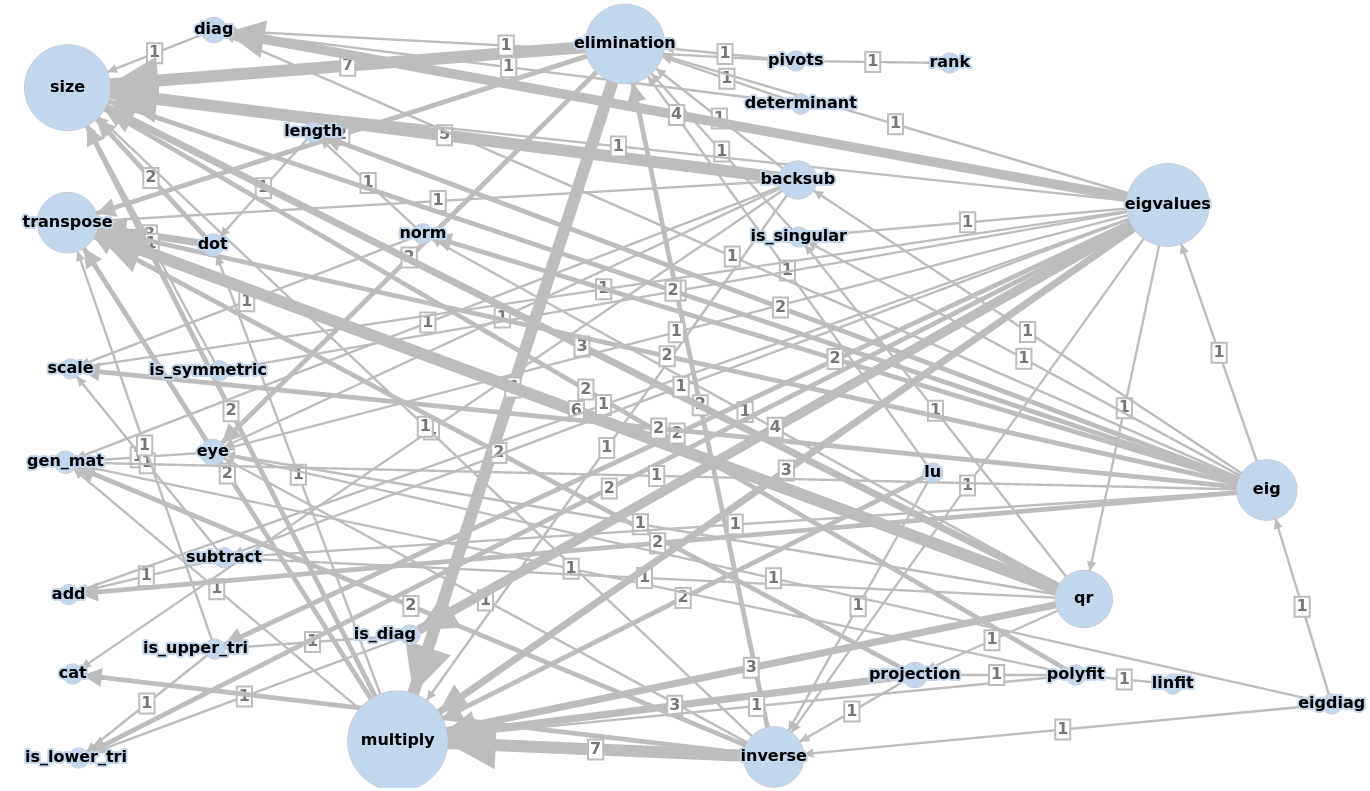
The dependencies among the methods are depicted by a weighted graph:
back to project main page
back to home
# Known bugs:
from copy import deepcopy as dc
from math import sqrt
def gen_mat(size, values=[0], kind='full'):
if type(size) is int:
size = [size, size]
if len(values) == 1:
values = [values[0] for val in range(max(size))]
elif len(values) < max(size):
values += [0 for val in range(max(size)-len(values))]
generated_mat = []
for i in range(size[0]):
row = []
for j in range(size[1]):
if (kind == 'diag' and j!=i) or (kind == 'upper' and j<=i) or (kind == 'lower' and j>=i):
row.append(0)
elif kind == 'diag':
row.append(values[j])
elif j>=i:
row.append(values[j-i])
elif j<i:
row.append(values[i-j])
generated_mat.append(row)
return Mat(generated_mat)
def eye(size):
return gen_mat(size, values=[1], kind='diag')
def cat(A, B, axis=0):
if axis == 0:
concatenated = Mat(A.data + B.data)
elif axis == 1:
concatenated = Mat([rows[0]+rows[1] for rows in zip(A.data, B.data)])
return concatenated
def print_mat(A, round_dp=99):
for row in A.data:
rounded = [round(j,round_dp) for j in row]
print(rounded)
print()
def vandermonde(n_rows, order=1):
A = gen_mat([n_rows, 1])
for i in range(n_rows):
orders = []
for exponent in range(order+1):
orders.append(i**exponent)
A.data[i] = orders
return A
class Mat:
def __init__(self, data):
self.data = data
def transpose(self):
transposed = []
for i, row in enumerate(self.data):
for j, col in enumerate(row):
# first time through, make new row for each old column
if i == 0:
transposed.append([col])
else:
# append to newly created rows
transposed[j].append(col)
return Mat(transposed)
def ind(self, i=None, j=None):
if isinstance(i, int) and not isinstance(j, int):
return Mat([self.data[i]])
elif isinstance(j, int) and not isinstance(i, int):
return Mat([self.tr().data[j]]).tr()
elif isinstance(i, int) and isinstance(j, int):
return self.data[i][j]
def size(self, axis=2):
if axis == 0:
return len(self.data)
elif axis == 1:
return len(self.data[0])
elif axis == 2:
return [len(self.data), len(self.data[0])]
def make_scalar(self):
if max(self.size()) == 1:
return self.ind(0,0)
def is_square(self):
return self.size(0) == self.size(1)
def is_wide(self):
return self.size(0) < self.size(1)
def is_tall(self):
return self.size(0) > self.size(1)
def is_lower_tri(self):
for i, row in enumerate(self.data):
for col in range(i+1,len(row)):
if row[col] != 0:
return False
else:
return True
def is_upper_tri(self):
return self.tr().is_lower_tri()
def is_diag(self):
if self.is_lower_tri() and self.is_upper_tri():
return True
else:
return False
def is_symmetric(self):
for i in range(self.size(0)):
for j in range(i+1, self.size(0)):
if self.ind(i,j) != self.ind(i,j):
return False
else:
return True
def tile(self, axes=[1,1]):
B = dc(self)
for j in range(axes[1]-1):
self = cat(self, B, axis=1)
B = dc(self)
for i in range(axes[0]-1):
self = cat(self, B, axis=0)
return self
def function_elwise(self, function, B=None):
C = gen_mat(self.size())
for i in range(self.size(0)):
for j in range(self.size(1)):
if B:
C.data[i][j] = function(self.ind(i,j), B.ind(i,j))
else:
C.data[i][j] = function(self.ind(i,j))
return C
def function_choice(self, B, functions):
if isinstance(B, Mat) == False:
return self.function_elwise(functions[0])
return self.function_elwise(functions[1], B)
def add(self, B):
return self.function_choice(B, [lambda x: x+B, lambda x, y: x+y])
def subtract(self, B):
return self.function_choice(B, [lambda x: x-B, lambda x, y: x-y])
def multiply_elwise(self, B):
return self.function_choice(B, [lambda x: x*B, lambda x, y: x*y])
def div_elwise(self, B):
return self.function_choice(B, [lambda x: x/B, lambda x, y: x/y])
def dot(self, new_mat):
# make both vectors rows with transpose
if self.size(0) != 1:
self = self.tr()
if new_mat.size(0) != 1:
new_mat = new_mat.tr()
dot_prod = []
for cols in zip(self.data[0], new_mat.data[0]):
dot_prod.append(cols[0]*cols[1])
dot_prod = sum(dot_prod)
return dot_prod
def length(self):
return sqrt(self.dot(self))
def norm(self):
if self.length() != 0:
self = self.div_elwise(self.length())
return self
def multiply(self, new_mat):
# preallocate empty matrix
multiplied = gen_mat([self.size(0), new_mat.size(1)])
# transpose one matrix, take a bunch of dot products
new_mat = new_mat.tr()
for i, row in enumerate(self.data):
tmp_row = Mat([row])
for j, col in enumerate(new_mat.data):
# enter the dot product into our final matrix
multiplied.data[i][j] = tmp_row.dot(Mat([col]))
return multiplied
def diag(self):
diag_vals = []
for idx in range(min(self.size())):
diag_vals.append(self.ind(idx,idx))
return diag_vals
def elimination(self):
# should do some row exchanges for numerical stability...
# we assume the matrix is invertible
singular = False
# size of elimination and perumtation matrices
mat_size = [self.size(0)]*2
# create identity matrix which we'll turn into an E matrix
E = eye(mat_size)
# create a permutation matrix for row exchanges
P = eye(mat_size)
U = dc(self)
pivot_count = 0
row_exchange_count = 0
for idx in range(U.size(0)-1):
for sub_row in range(idx+1, U.size(0)):
# create elimination mat
nextE = eye(mat_size)
nextP = eye(mat_size)
# handle a zero in the pivot position
if U.data[idx][pivot_count] == 0:
row_exchange_count += 1
# look for a non-zero value to use as the pivot
options = [row[pivot_count] for row in U.data[sub_row:]]
exchange = sub_row + options.index(max(options, key=abs))
# build and apply a purmutation matrix
nextP.data[idx][pivot_count] = 0
nextP.data[idx][exchange] = 1
nextP.data[exchange][exchange] = 0
nextP.data[exchange][pivot_count] = 1
U = nextP.multiply(U)
P = nextP.multiply(P)
# check if the permutation avoided a zero in the pivot position
if U.data[idx][idx] == 0:
singular = True
# undo the row exchanges that failed
row_exchange_count -= 1
U = nextP.tr().multiply(U)
P = nextP.tr().multiply(P)
# move on to the next column
break
# determine how much to subtract to create a zero
ratio = U.data[sub_row][pivot_count]/U.data[idx][pivot_count]
# create the elimination matrix for this step
nextE.data[sub_row][idx] = -ratio
# apply the elimination step to U
U = nextE.multiply(U)
# update the overall E
E = nextE.multiply(E)
pivot_count += 1
# If self was a 1x1 matrix, the above loops didn't happen. Take the
# reciprocal of the number:
if U.size(0) == 1 and U.size(1) == 2:
if U.ind(0,0) != 0:
U.data[0] = [1/U.ind(0,0), 1]
i = -1
# check if the matrix is square
if U.size(1) == U.size(0):
# check if the permutation avoided a zero in the pivot position
if U.data[idx+1][idx+1] == 0:
singular = True
return P, E, self, U, singular, row_exchange_count
def backsub(self, b):
augmented = cat(self, b, axis=1)
_, _, _, U, _, _ = augmented.elimination()
coeff = []
for idx in range(-1, -(U.size(0)+1), -1):
if idx < -1:
E = eye([U.size(0)+1, U.size(1)])
E.data[idx][U.size(1)-1] = -1*(coeff[-1])
U = U.multiply(E)
row = U.data[idx]
# check solution possibilities
if row[idx-1] == 0 and row[-1] != 0:
print('No solution!')
return None
elif row[idx-1] == 0 and row[-1] == 0:
print('Infinite solutions!')
coeff.append(1)
else:
coeff.append(row[-1]/row[idx-1])
coeffs = list(reversed(coeff))
return Mat([coeffs]).tr()
def pivots(self):
_, _, _, U, _, _ = self.elimination()
# extract the first non-zero from each row - track the column number
U = U.tr()
pivots = {}
found = []
for j, col in enumerate(U.data):
piv_pos = sum(list(map(bool, col)))
if piv_pos not in found:
found.append(piv_pos)
pivots[j] = col[piv_pos-1]
return pivots
def rank(self):
return len(self.pivots())
def is_singular(self):
_, _, _, _, singular, _ = self.elimination()
return singular
def determinant(self):
# find U
_, _, _, U, _, row_exchange_count = self.elimination()
# muliply the pivots
det = 1
diag_vals = U.diag()
for val in diag_vals:
det *= val
# if an odd number of row exchanges, multiply determinant by minus one
if row_exchange_count % 2:
det *= -1
return det
def pivot_sign_code(self):
'''Returns number between 0 and 7 according to signs of pivots. We do
this by constructing a 3-bit binary number, where each bit represents
the presence/absence of negative, zero, or positive pivots, and then
converting from binary to a base 10 integer.'''
pivot_info = self.pivots().items()
neg = int(any(piv[1] < 0 for piv in pivot_info))
semi = int(len(pivot_info) < self.size(1))
pos = int(any(piv[1] > 0 for piv in pivot_info))
return int(str(neg) + str(semi) + str(pos), 2)
def is_negdef(self):
return self.pivot_sign_code() == 4
def is_negsemidef(self):
return self.pivot_sign_code() == 6
def is_possemidef(self):
return self.pivot_sign_code() == 3
def is_posdef(self):
return self.pivot_sign_code() == 1
def inverse(self):
mat_size = self.size()
# create [A I]
I = eye(mat_size)
augmented = cat(self, I, axis=1)
# perform elimination to get to [U ~inv]
_, _, _, U, singular, _ = augmented.elimination()
if singular:
print('Matrix is singular!')
return None
# seperate augmented into U and ~inv
tmp_fU = Mat([Urow[0:mat_size[1]] for Urow in U.data])
tmp_inv = Mat([Urow[mat_size[1]:] for Urow in U.data])
# create anti-diag I
antiI = gen_mat(mat_size)
for i, j in enumerate(reversed(range(mat_size[1]))):
antiI.data[i][j] = 1
# multiply U and ~inv on both sides by anti-diag I
fU = antiI.multiply(tmp_fU).multiply(antiI)
f_tmp_inv = antiI.multiply(tmp_inv).multiply(antiI)
# put fU back into [fU f~inv]
augmented = cat(fU, f_tmp_inv, axis=1)
# perform elimination again to get to [cI cA^-1]
_, _, _, U, _, _ = augmented.elimination()
# divide each row by c to get [I A^-1]
div = gen_mat(mat_size)
for idx in range(mat_size[0]):
div.data[idx][idx] = 1/U.ind(idx,idx)
inv = div.multiply(U)
# flip back
inv = antiI.multiply(inv)
for idx in range(mat_size[1]):
inv.data[idx] = inv.data[idx][mat_size[1]:]
inv = inv.multiply(antiI)
return inv
def lu(self):
P, E, A, U, _, _ = self.elimination()
E = P.multiply(E)
L = P.multiply(E.inverse())
return A, P, L, U
def projection(self):
# P = A((A'A)^-1)A'
AtA_inv = (self.tr().multiply(self)).inverse()
for_x = AtA_inv.multiply(self.tr())
Projection = self.multiply(for_x)
return Projection, for_x
def project_onto_A(self, A):
_, for_x = A.projection()
projected = for_x.multiply(self)
return projected
def polyfit(self, order=1):
V = vandermonde(self.size(0), order=order)
# fit model to b
return self.project_onto_A(V)
def linfit(self):
return self.polyfit()
def qr(self):
if self.is_singular():
print('Matrix is singular!')
return self, None, None
A = self.tr()
Q = dc(A)
I = eye(A.size())
# projection orthogonal to column
for col in range(Q.size(0)-1):
Col = dc(Mat([Q.data[col]]))
P, _ = Col.tr().projection()
P = I.subtract(P)
# project and put into matrix Q
for col2 in range(col+1, Q.size(0)):
Col = dc(Mat([Q.data[col2]]))
q = P.multiply(Col.tr()).tr()
Q.data[col2] = q.data[0]
# normalise to unit length
for x, q in enumerate(Q.data):
q = Mat([q])
q = q.norm()
Q.data[x] = q.data[0]
A = A.tr()
R = Q.multiply(A)
Q = Q.tr()
A = Q.multiply(R)
return A, Q, R
def eigvalues(self, epsilon = 0.0001, max_its=100):
if not (self.is_symmetric() or self.is_lower_tri() or self.is_upper_tri()):
print('Matrix is not symmetric or triangular and may therefore have complex eigenvalues which this method cannot handle. Interpret results with care!')
if self.is_upper_tri() or self.is_lower_tri():
return Mat([self.diag()])
if self.is_singular():
print('Matrix is singular!')
return None
old_eig = 0
final_eigs = []
for its in range(max_its):
# obtain off diagonal zeros
_, E, _, _, _, _ = self.elimination()
Einv = E.inverse()
A = E.multiply(self).multiply(Einv)
# shift A by -cI, where c is last diag
shift = eye(A.size()).multiply_elwise(old_eig)
# QR factorisation
A = A.subtract(shift)
_, Q, R = A.qr()
A = R.multiply(Q)
A = A.add(shift)
current_eig = A.diag()[-1]
diff = old_eig - current_eig
old_eig = current_eig
if abs(diff) < epsilon:
if min(A.size()) == 2:
final_eigs += A.diag()
return Mat([final_eigs])
else:
final_eigs.append(current_eig)
A = A.data[:-1]
A = [row[:-1] for row in A]
A = Mat(A)
old_eig = A.diag()[-1]
else:
print('Did not converge!')
return None
def eig(self, epsilon=0.0001, max_its=100):
if self.is_singular():
print('Matrix is singular!')
return None, None
evals = self.eigvalues()
evects = []
for evalue in evals.data[0]:
# ensure we don't destroy the diagonal completely
if evalue in self.diag():
evalue -= 1e-12
A_shifted = self.subtract(eye(self.size()).multiply_elwise(evalue))
# A_shifted_inv = A_shifted.inverse()
b = gen_mat([self.size(0),1], values=[1])
b = b.norm()
for its in range(max_its):
old_b = dc(b)
b = A_shifted.backsub(b)
# b = A_shifted_inv.multiply(b)
b = b.norm()
diff1 = b.subtract(old_b)
diff2 = b.subtract(old_b.multiply_elwise(-1))
if diff2.length() or diff2.length() < epsilon:
evects.append(b.tr().data[0])
break
evects = Mat(evects).tr()
return evects, evals
def eigdiag(self):
evects, evals = self.eig()
eigval_mat = gen_mat(self.size(), values=evals.data[0], kind='diag')
if self.is_symmetric():
evectsinv = evects.tr()
else:
evectsinv = evects.inverse()
return evects, eigval_mat, evectsinvback to project main page
back to home